Layer number regulated intra-layer magnetism

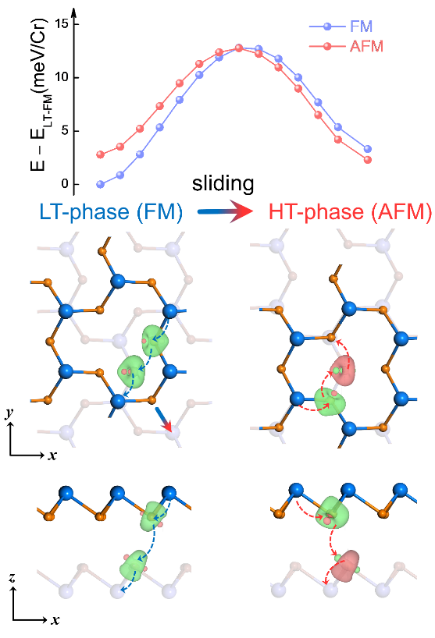
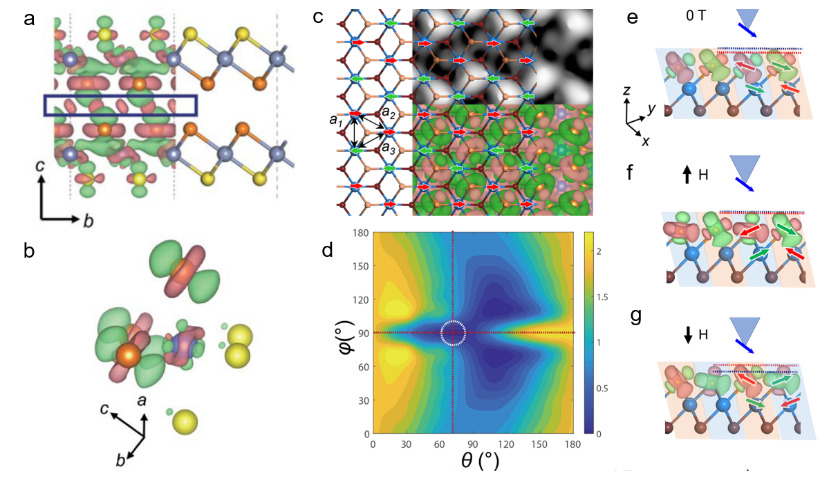
Fig.1 Layer number regulated intra-layer magnetism. a-b: differential charge density between layers. Red represents the accumulation of charge in the interlayer region after the two layers are stacked on top of each other. c-d: Single layer CrTe2 zigzag antiferromagnetic ground state and easy magnetization axis direction. e-g: Spin reorientation transformation of CrTe2 monolayer.
.
Nature Communications
Spin mapping of intralayer antiferromagnetism and field-induced spin reorientation in monolayer CrTe2
Charge redistribution induced by interlayer interaction is relatively small at the vdW gap of a CrI3 bilayer in comparison with other bilayers like BP, Te, PtSe2, PtS2, and CrS2, suggesting a limited overlap of interlayer wave functions in the CrI3 bilayer. It is exceptional that such a small overlap could even appreciably affect the interlayer magnetism through direct exchange between two interlayer I atoms separated by 4.20 Å2.
A question then arises of how do strongly overlapped interlayer wave functions affect interlayer magnetism and whether there are any generalized spin-exchange coupling mechanisms solely for such a noncovalent interaction. The interlayer differential charge density shows that the interlayer electron coupling of of CrX2(X = S, Se, Te) systems is significantly stronger than that of CrI3. It is expected that different interlayer magnetic coupling mechanisms exist in CrX2. The bulk phase of this kind of material shows ferromagnetism, and many studies speculate that the single layer should also be the ferromagnetic ground state. However, the theoretical prediction of the researchers found that the single layer of this kind of material is striped antiferromagnetic ground state. The in-plane magnetic orders of CrX2 mono and few layers are tunable between striped antiferromagnetic (sAFM) and ferromagnetic (FM) orders by manipulating charge transfer between Cr t2g and eg orbitals. Such charge transfer is realizable through interlayer coupling, direct charge doping, or substituting S with Cl atoms[1,2].
However, due to the fact that antiferromagnetic orders usually do not exhibit macroscopic magnetic moments, experimental detection is very difficult, and the antiferromagnetic ground state of CrX2(X=S,Se,Te) materials mentioned in the above theoretical prediction are still lacking of experimental evidence in the two-dimensional limit. By combining spin polarised scanning tunnelling microscopy and first-principles calculations, we investigate the magnetism of vdW ML CrTe2, which has been successfully grown through molecular-beam epitaxy. We observe a stable antiferromagnetic (AFM) order at the atomic scale in the ML crystal, whose bulk is ferromagnetic, and correlate its imaged zigzag spin texture with the atomic lattice structure. confirming the theoretical prediction of the researchers (FIG. 1 c). Previous studies of two-dimensional magnetic materials usually assumed that the material’s easy magnetization axis was along the conventional lattice base vector or out of plane direction. The researchers calculated that the magnetic moment direction of the CrTe2 single layer was in the y-z plane at an Angle of 70 degrees from the z direction (FIG. 1 d), resulting in a novel spin reorientation transition mode under magnetic field (FIG. 1 e-g). The real space intrinsic antiferromagnetic order discovered and confirmed in this study, the magnetic order transformation in the single-layer limit, and the spin reorientation under external magnetic fields have not been previously reported before[3].
1. C. Wang, X. Zhou, Y. Pan, J. Qiao, X. Kong, C.-C. Kaun, and W. Ji, Layer and Doping Tunable Ferromagnetic Order in Two-Dimensional CrS2 Layers, Phys. Rev. B 97, 245409 (2018).
2. Wang, C. et al. Bethe-Slater-curve-like behavior and interlayer spin-exchange coupling mechanisms in two-dimensional magnetic bilayers. Phys. Rev. B 102, 020402 (2020).
3. Xian, J.-J. et al. Spin mapping of intralayer antiferromagnetism and field-induced spin reorientation in monolayer CrTe2. Nature Communications 13, 257 (2022)